SCHÖNHEIT DER LOGIK BEIM SODUKO CHESS

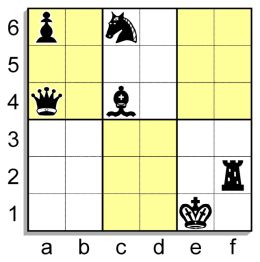
Beim Soduko Chess werden die Felder im Diagramm mit Schachfiguren ausgefüllt. Mit dem Schach­spiel selbst hat das aber nichts zu tun – man muss also keinerlei Schachregeln kennen. Es genügen geistige Kreativität und logisches Denkvermögen. Und so geht’s: Füllen Sie die leeren Felder im Diagramm mit den Buchstaben B, S, L, T, D und K (für Bauer, Springer, Läufer, Turm, Dame und König) so aus, dass in jeder waagrechten und senkrechten Felderreihe, auf beiden Diagonalen und in jedem 2x3-Rechteck jede Figur nur je einmal vorkommt.  Auf der Diagonalen f1-a6 könnte ein Springer (S) auf d3 stehen. Dann aber passt kein S mehr ins untere rechte 2x3-Rechteck. – Auf der Diagonalen könnte ein Springer auch auf e2 stehen. Dann aber muss im unteren mittleren Rechteck ein S auf d1 sein. Nun lässt sich auf der Diagonalen a1-f6 jedoch kein S mehr unterbringen. – Sb5 auf der Diagonalen? Dann aber lassen sich auf dem Rest dieser Diagonalen T, D und K nicht mehr korrekt unterbringen. Also: Sf1.  Dd3 auf der Diagonalen? Dann passt keine Dame mehr ins untere rechte Rechteck. Also: De2. Nun passt ins untere mittlere Rechteck ein S nur noch auf d2. Also: Sd2. – Se4 auf der e-Reihe? Dann würde kein S mehr auf die Diagonale a1-f6 passen. Also: Se5. Daraus ergibt sich für das obere linke Rechteck: Sb4. Der letzte Springer passt jetzt nur noch auf a3. Also: Sa3. Unter Beachtung der Diagonalen f1-a6 ergibt sich Ld1. – T und K müssen diagonal auf d3/b5 stehen, also kann auf Feld b3 (in Reihe 3) weder ein T noch ein K sein. In Reihe 3 müssen außerdem B/L auf e3/f3 sein, und demnach kann eine Dame in Reihe 3 nur noch auf b3 stehen. Also: Db3. Daraus ergibt sich fürs untere mittlere Rechteck: Dc1. Daraus folgt für die Diagonale a1-f6: Df6. Und daraus ergibt sich die sechste

und letzte Dame: Dd5.  Wegen B/L auf e3/f3 ergibt sich fürs untere mittlere Rechteck: Bc2. Daraus folgt für die d-Felderreihe: Bd4. Daraus folgt fürs obere rechte Rechteck: Bf5. Daraus folgt fürs untere rechte Rechteck: Be3. Und Lf3. Für die senkrechte f-Reihe ergibt sich nun Kf4. Für die e-Reihe ergibt sich Le6. Und Te4. Diagonal auf a1-f6 ergibt sich Lb2. Und Kc3. Und dadurch noch Ta1. – Für Reihe 3 ergibt sich Td3 und diagonal f1-a6 Kb5. Aus Kb5 folgt Ka2. Für Reihe 1 ergibt sich Bb1, für die b-Reihe Tb6, für die d-Reihe Kd6 und für die a-Reihe La5. Restbesetzung: Tc5.

Peter Krystufek
Begründer der Schachfiguren-Problemreihe Soduko Chess November 2005